Derivada 

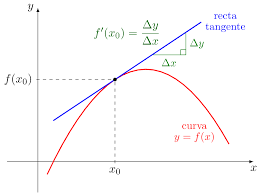
De la función f(x), es aquella función denotada por f(x) tal que su valor de función en cualquier numero x en el dominio de f(x) esta dada por 

f´(x)=lim f ( x + h ) - f ( x ) / h    h->0

Teoremas de derivadas 

Es necesario conocer y comprender la definición de derivada , ya que sirven para poder calcular la derivada de cualquier función mediante formulas.

Teorema 1

Si f ( x ) =  C ( C una constante ) para toda X, entonces f´ ( x ) = 0

Teorema 2

Si f ( x ) = x ^ n      N es un entero positivo,  entonces f´ ( x ) =  nx ^ n-1 

Teorema 3

Si g ( x ) = C f ( x ), C una constante,  entonces g´ ( x ) = C f´ ( x ),  si f´ ( x ) existe 

Teorema 4

Si f ( x ) y g ( x ) son dos funciones tales que f´ ( x ) y g´ ( x ) existen,  entonces Dx [ f ( x ) + g ( x ) ] = Dx f ( x ) + Dx g ( x )

Teorema 5 

Si f ( x ) y g ( x ) son funciones cuyas derivadas existen , entonces Dx [ f ( x ) g ( x ) ] = f´ ( x ) g ( x ) + g´ ( x ) f ( x ) 

Teorema 6 

Si f ( x ) y g ( x ) sus funciones donde g ( x ) = 0 y cuyas derivadas existen , entonces Dx [ f ( x ) / g ( x ) ] = g ( x ) f´ ( x ) - f ( x ) g´ ( x ) / [ g ( x )]^2

Teorema 7 

Si n es un racional positivo es Dx ( x^- n ) = - nx ^-n-1